6.5. The Alphas Parameters

The model objective function consists of four main components; one that defines how the model can vary from the reference model, and one for each of the allowed gradients in the x, y and z directions. Each of these four components has a coefficient, denoted by α, that controls their relative importance in the regularization \(\phi_m (\mathbf{m})\).

(1)\[\begin{split}\phi_m(\mathbf{m}) = &\color{blue}{\alpha_s} ||\mathbf{W}_s\;\mathbf{R}_s(\mathbf{m}-\mathbf{m}_{ref})||_2^2 +\\ &\color{blue}{\alpha_x} ||\mathbf{W}_x\;\mathbf{R}_x \; \mathbf{G}_x(\mathbf{m}-\mathbf{m}_{ref})||_2^2 +\\ &\color{blue}{\alpha_y} ||\mathbf{W}_y\;\mathbf{R}_y \; \mathbf{G}_y(\mathbf{m}-\mathbf{m}_{ref})||_2^2 +\\ &\color{blue}{\alpha_z} ||\mathbf{W}_z\;\mathbf{R}_z \; \mathbf{G}_z(\mathbf{m}-\mathbf{m}_{ref})||_2^2\end{split}\]

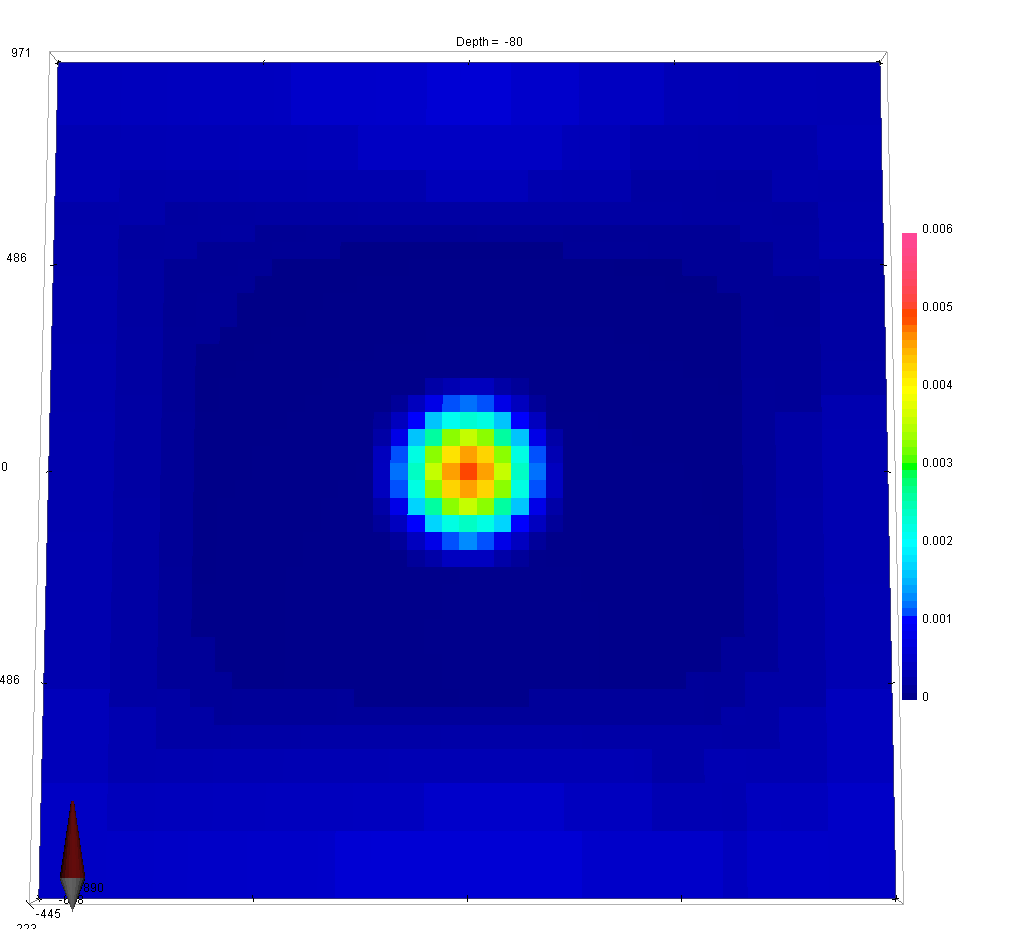
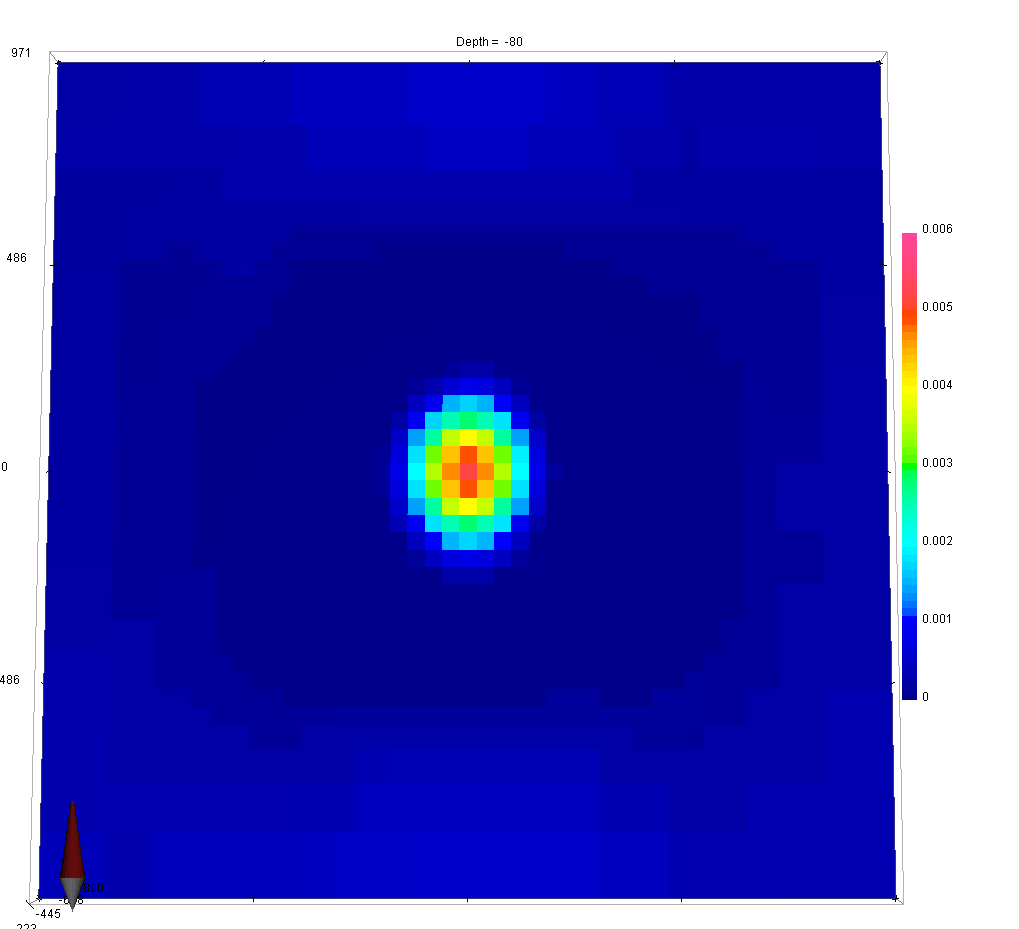
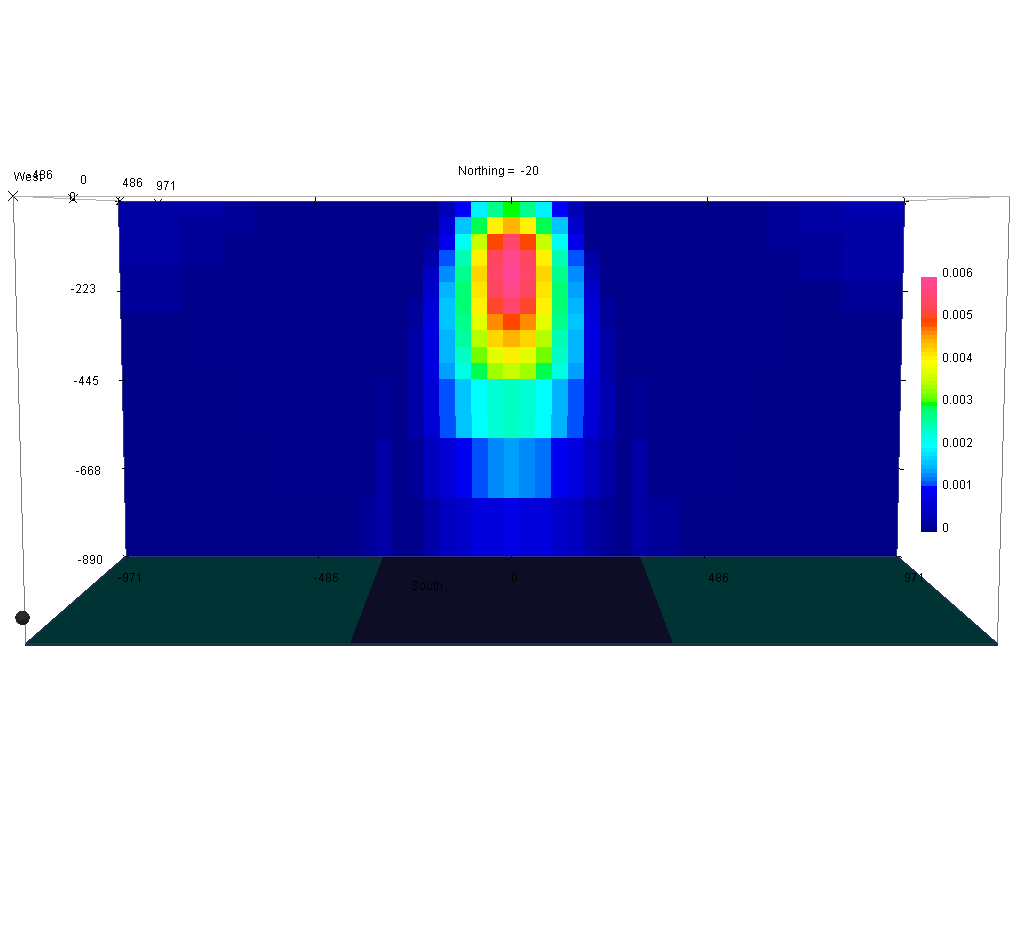
In this example, we demonstrate the effect that each α value has on the solution.

αs = 1/dx2, αx=αy=αz=1
αs / 10
αx x 10
αy x 10
αz x 10

As a general rule of thumb, larger \(\alpha_x\), \(\alpha_y\) and \(\alpha_z\) results in an increased smoothing in the corresponding direction, while reducing \(\alpha_s\) results in an overall smoother model.

Tip

In order to get equal contribution from all four components making up \(\phi_m(\mathbf{m})\), set \(\alpha_s=\frac{1}{h^2}\), where h represent the cell size dimension in the core region. If the mesh cells are not cubic, α values should be adjusted accordingly (smaller h => reduced α)

It is sometimes useful to think of the α values in terms of length scales:

\[L_x = \sqrt{\frac{\alpha_x}{\alpha_s}}, \quad L_y = \sqrt{\frac{\alpha_y}{\alpha_s}}, \quad L_z = \sqrt{\frac{\alpha_z}{\alpha_s}}\]

These length scales can be adjusted to reflect a priori information about the general trend expected from the geology.

Important

In most inversion codes, the default α values are: \(\left[ \alpha_s=1e-4, \alpha_x=\alpha_y=\alpha_z=1 \right]\).